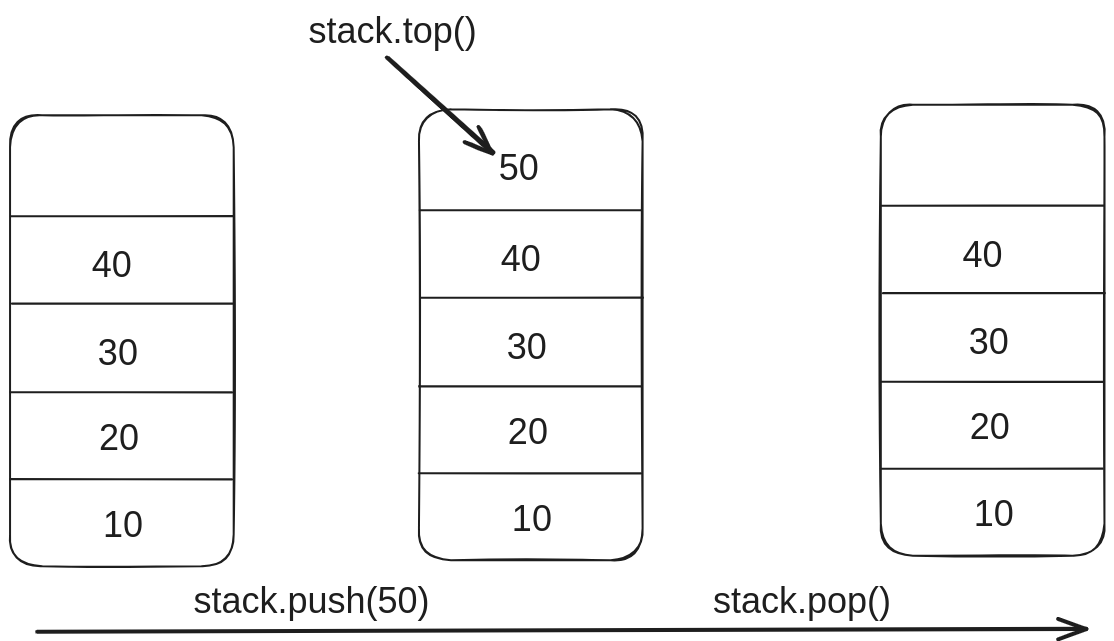
Stack
- A stack is an ADT that follows the Last-In-First-Out (LIFO) principle. It provides operations like push (to add an item to the top of the stack) and pop (to remove and return the top item).
When To Use Stack?
It follows the Last-In-First-Out (LIFO) principle, which means that the last element added to the stack is the first one to be removed.
They all have one characteristic in common which is that the last element inserted is the first one to be deleted.
1. Function Call Stack
- In programming, function calls are often managed using a stack. When a function is called, its local variables and execution context are pushed onto the stack, and when the function returns, they are popped off the stack. This ensures that the program can return to the correct execution context after a function call.
2. Expression Evaluation
- Stacks are useful for evaluating expressions, including arithmetic expressions and expressions with nested parentheses. You can use a stack to keep track of operators and operands and apply operators in the correct order.
3. Undo/Redo Functionality
- Implementing undo and redo functionality in applications, such as text editors or drawing programs, can be done using a stack. Each action is pushed onto the stack, allowing users to undo and redo their actions by popping from and pushing onto the stack.
4. Parsing and Syntax Checking
- When parsing and validating input, especially in programming languages or markup languages, a stack can be used to ensure that opening and closing symbols (e.g., parentheses, brackets, and tags) are balanced and properly nested.
5. Backtracking Algorithms
- Certain algorithms, like depth-first search (DFS) in graph traversal or recursive algorithms, can benefit from using a stack to keep track of the current state and backtrack when necessary.
6. History Tracking
- Stacks can be used to maintain a history of user actions, such as in web browsers, allowing users to navigate backward and forward through their browsing history.
7. Solving Problems with Constraints:
- Certain problems, like the Tower of Hanoi puzzle or maze solving, can be efficiently solved using a stack to keep track of intermediate steps and decisions.
8. Postfix (Reverse Polish) Notation:
- When working with postfix notation, which is a way to represent mathematical expressions without parentheses, stacks are often used to evaluate expressions efficiently.
Stack examples
프로그래머스 스쿨 - 주식가격
solution
brute-force solution
- Time Complexity : O(N^2) -> two for loops
- Memory Complexity : O(N) -> additional list answer
def solution(prices):
answer = []
for cur_idx, cur_price in enumerate(prices):
# every price start with 0 time
answer.append(0)
for future_idx, future_price in enumerate(prices[cur_idx+1:], start=cur_idx+1):
# every loop, we add (time) 1 to the answer list
answer[-1] += 1
if cur_price > future_price:
break
return answer
result = solution([1,2,3,2,3])
print(result)
assert result == [4,3,1,1,0]Stack solution
- Time Complexity : O(N)
- Memory Complexity : O(N)
def solution(prices):
answer = [0]*len(prices)
stack = [] # in this stack, we keep the indices that didn't decrease from it's index to the end of the pirces list
for cur_price_idx, cur_price in enumerate(prices):
# price decreasing -> update answer : if current price is lower than last price (prices[stack[-1]])
while stack and cur_price < prices[stack[-1]]:
# pop current(will be replaced) head idx
old_head_idx = stack.pop()
# since we found the answer for price for old_head_idx, we set value for that index
answer[old_head_idx] = cur_price_idx - old_head_idx
# price increaseing or stay same -> add current idx to stack (this stack )
stack.append(cur_price_idx)
print(f"stack: {stack}")
print(f"answer: {answer}")
# now we have
# stack : keep (the indices of) prices in non-decreasing order e.g. [1 2 2 3]
# answer : for the ones we know the answer has value in it other than zeros,
# for the ones we haven't found out we will update in below while loop
while stack:
old_head_idx = stack.pop()
answer[old_head_idx] = len(prices) - 1 - old_head_idx
print(f"stack: {stack}")
print(f"answer: {answer}")
return answer
result = solution([1,2,3,2,3])
print(result)
assert result == [4,3,1,1,0]Valid Parentheses - LeetCode
solution
- Time Complexity : O(N)
Memory Complexity : O(N)
- worst case : all characters are opening characters then nothing will be popped until the end
class Solution:
def isValid(self, s: str) -> bool:
stack = []
close2open = {
")": "(",
"}": "{",
"]": "[",
}
for char in s:
if char in close2open.values():
stack.append(char)
else:
if not stack:
return False
pop_char = stack.pop()
if pop_char != close2open[char]:
return False
continue
return len(stack) == 0
assert Solution().isValid("()[]{}") == True #
assert Solution().isValid("()") == True
assert Solution().isValid("(]") == False